• 奇偶链表：

    • 题目重述：将一个链表的编号奇偶的放在一起，使用原地算法。(不能开辟空间，在原链表操作)

    • 难点：如何保持相对顺序的情况下一起移动链表的结点。

    • 解决办法：将奇链表放在一个节点里，偶链表放在一个节点里。（定义双指针引用）

      定义一个evenhead链表引用，始终保持=even，所以最后就有

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    ListNode even = head.hext;
    ListNode odd  = head;
    ListNode evenhead = even;
    while(even!==null&&even.next==null){
        odd.next=even.next;//覆盖偶数节点(第一步)
        odd=odd.next;//让奇数节点往后走一步
      event.next=odd.next;//跳过中间的奇数节点
        event=event.next;//让偶数节点往后走一步
    }
    odd.next=evenhead;//连接起来
    return odd;//伪代码

  • 分割链表

    • 题目重述：给定一个链表和一个x，将链表元素小于或等于x的放在x的左边，大于x的放在x的右边。

    • 难点：移动链表，遍历链表

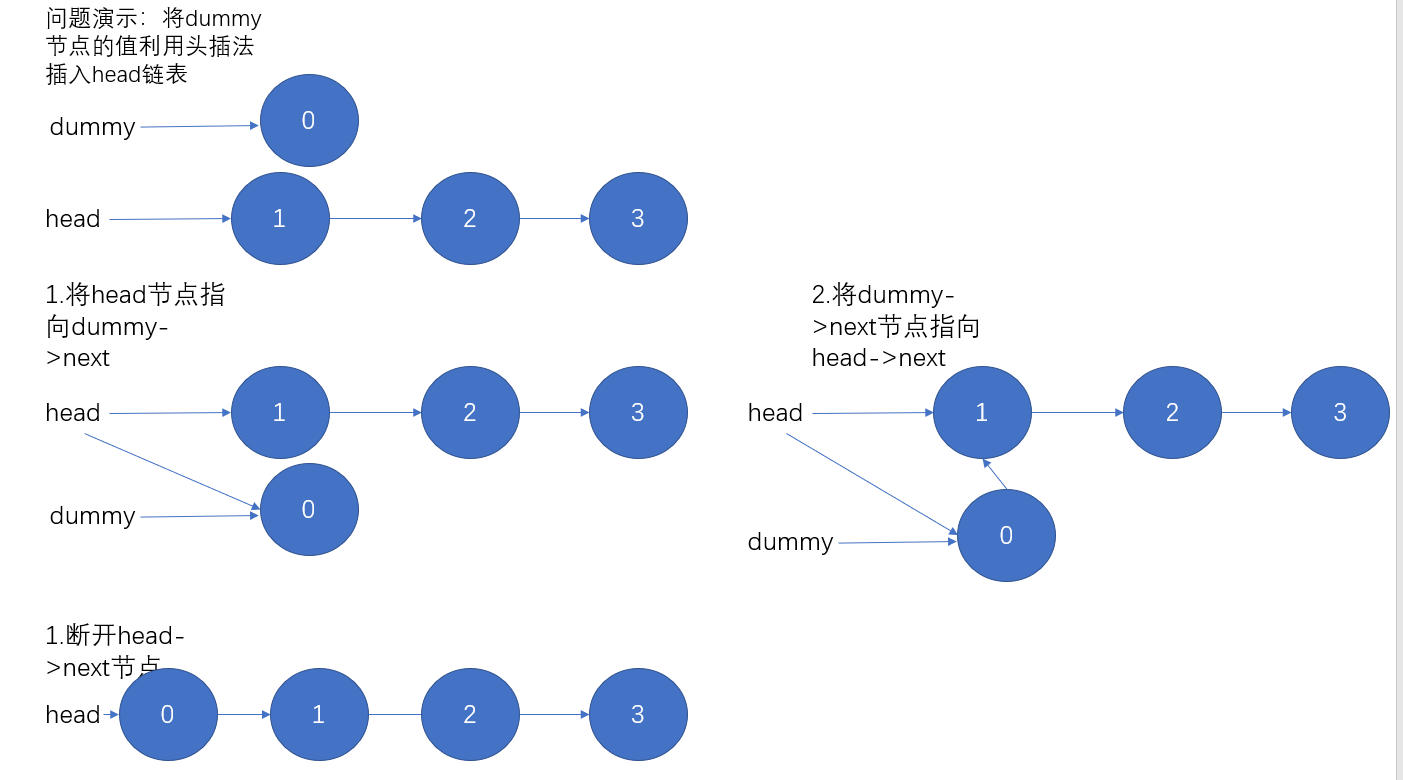
    • 步骤：见下图头插法

    • 解决办法：链表的头插法

      （头插法这里我想了很久，为了把这个事情说清楚我们做一个步骤图来说明一下

      img

  • 环路检测：

    • 题目重述：返回一个环路链表的开头结点

    • 难点：1.快慢指针相遇问题（快指针跑两步，慢指针走一步），2.找入口

    • 步骤：1.先找相遇点（有无环）。2.再找入口

    • 解决办法：先证明一下相遇的情况，再根据结果进行一个编写。

      相遇了则证明有环，数学证明发现一个从相遇点一步一步走，一个从头一步一步走，再次相遇的时候就是环的入口。所以我们先要找到相遇点、再让其同时一步一步走就可以。

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      if(head==null){
          return head;
      }
      ListNOde fast=head;
      ListNode slow=head;
      while(fast!=null){    
          fast=fast.next.next;
        slow=slow.next;
          if(fast==slow){
              break;
          }
      }//第一次相遇，证明有环
      fast=head;
      while(fast!=null&&fast.next!=null){
          fast=fast.next;
          slow=slow.next;
          if(fast==slow){
              break;
          }
      }
      return fast;
      1
      2
      3
      4
      5
      6
      7
      8
      //如果没有环我们需要改变一下第一个while里的if的条件
      while(fas!=null){
        if(fast==null||fast.next==null) return null;
        ···
        ···
      }
      ···
      ···

      后面的拓展：如果要没有环要选择返回null